Примеры цилиндрических суставов. Классификация суставов и их общая характеристика

Примеры цилиндрических суставов. Классификация суставов и их общая характеристика

Классификацию суставов можно проводить по следующим принципам :
1) по числу суставных поверхностей,
2) по форме суставных поверхностей и
3) по функции.

По числу суставных поверхностей различают:
1. Простой сустав (art. simplex) , имеющий только 2 суставные поверхности, например межфаланговые суставы.
2. Сложный сустав (art. composite) , имеющий более двух сочленовных поверхностей, например локтевой сустав. Сложный сустав состоит из нескольких простых сочленений, в которых движения могут совершаться отдельно. Наличие в сложном суставе нескольких сочленений обусловливает общность их связок.
3. Комплексный сустав (art. complexa) , содержащий внутрисуставной хрящ, который разделяет сустав на две камеры (двухкамерный сустав). Деление на камеры происходит или полностью, если внутрисуставной хрящ имеет форму диска (например, в височно-нижнечелюстном суставе), или неполностью, если хрящ приобретает форму полулунного мениска (например, в коленном суставе).
4. Комбинированный сустав представляет комбинацию нескольких изолированных друг от друга суставов, расположенных отдельно друг от друга, но функционирующих вместе. Таковы, например, оба височно-нижнечелюстных сустава, проксимальный и дистальный лучелоктевые суставы и др.
Так как комбинированный сустав представляет функциональное сочетание двух или более анатомически отдельных сочленений, то этим он отличается от сложного и комплексного суставов, каждый из которых, будучи анатомически единым, слагается из функционально различных соединений.

Примеры цилиндрических карт. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ В ЗАВИСИМОСТИ ОТ ОРИЕНТИРОВАНИЯ ВСПОМОГАТЕЛЬНОЙ КАРТОГРАФИЧЕСКОЙ ПОВЕРХНОСТИ

Нормальные проекции – плоскость проектирования касается земного шара в точке полюса или ось цилиндра (конуса) совпадает с осью вращения Земли (рис. 6.11).

Рис. 6.11. Нормальные (прямые) проекции

Поперечные проекции – плоскость проектирования касается экватора в какой-либо точке или ось цилиндра (конуса) совпадает с плоскостью экватора (рис. 6.12).

Рис. 6.12. Поперечные проекции

Косые проекции – плоскость проектирования касается земного шара в любой заданной точке (рис. 6.13).

Рис. 6.13. Косые проекции

Из косых и поперечных проекций наиболее часто используют косые и поперечные цилиндрические, азимутальные (перспективные) и псевдоазимутальные проекции. Поперечные азимутальные применяют для карт полушарий, косые – для территорий, имеющих округлую форму. Карты материков часто составляют в поперечных и косых азимутальных проекциях. Поперечно-цилиндрическая проекция Гаусса – Крюгера применяется для государственных топографических карт.

6.3. ВЫБОР ПРОЕКЦИЙ

На выбор проекций влияет много факторов, которые можно сгруппировать следующим образом:

• географические особенности картографируемой территории, ее положение на Земном шаре, размеры и конфигурация;
• назначение, масштаб и тематика карты, предполагаемый круг потребителей;
• условия и способы использования карты, задачи, которые будут решаться по карте, требования к точности результатов измерений;
• особенности самой проекции – величины искажений длин, площадей, углов и их распределение по территории, форма меридианов и параллелей, их симметричность, изображение полюсов, кривизна линий кратчайшего расстояния.

Первые три группы факторов задаются изначально, четвертая – зависит от них. Если составляется карта, предназначенная для навигации, обязательно должна быть использована равноугольная цилиндрическая проекция Меркатора. Если картографируется Антарктида, то почти наверняка будет принята нормальная (полярная) азимутальная проекция и т.д.
Значимость названных факторов может быть различной: в одном случае на первое место ставят наглядность (например, для настенной школьной карты), в другом – особенности использования карты (навигация), в третьем – положение территории на земном шаре (полярная область). Возможны любые комбинации, а следовательно – и разные варианты проекций. Тем более что выбор очень велик. Но все же можно указать некоторые предпочтительные и наиболее традиционные проекции.
Карты мира обычно составляют в цилиндрических, псевдоцилиндрических и поликонических проекциях. Для уменьшения искажений часто используют секущие цилиндры, а псевдоцилиндрические проекции иногда дают с разрывами на океанах.
Карты полушарий всегда строят в азимутальных проекциях. Для западного и восточного полушарий естественно брать поперечные (экваториальные), для северного и южного полушарий – нормальные (полярные), а в других случаях (например, для материкового и океанического полушарий) — косые азимутальные проекции.
Карты материков Европы, Азии, Северной Америки, Южной Америки, Австралии с Океанией чаще всего строят в равновеликих косых азимутальных проекциях, для Африки берут поперечные, а для Антарктиды – нормальные азимутальные.
Карты отдельных стран , административных областей, провинций, штатов выполняют в косых равноугольных и равновеликих конических или азимутальных проекциях, но многое зависит от конфигурации территории и ее положения на земном шаре. Для небольших по площади районов задача выбора проекции теряет актуальность, можно использовать разные равноугольные проекции, имея в виду, что искажения площадей на малых территориях почти неощутимы.
Топографические карты Украины создают в поперечно-цилиндрической проекции Гаусса, а США и многие другие западные страны – в универсальной поперечно-цилиндрической проекции Меркатора (сокращенно UТМ). Обе проекции близки по своим свойствам; по существу та и другая являются многополостными.
всегда даются исключительно в цилиндрической проекции Меркатора, а тематические карты морей и океанов создают в самых разнообразных, иногда довольно сложных проекциях. Например, для совместного показа Атлантического и Северного Ледовитого океанов применяют особые проекции с овальными изоколами, а для изображения всего Мирового океана – равновеликие проекции с разрывами на материках.
В любом случае при выборе проекции, в особенности для тематических карт, следует иметь в виду, что обычно искажения на карте минимальны в центре и быстро возрастают к краям. Кроме того, чем мельче масштаб карты и обширнее пространственный охват, тем большее внимание приходится уделять «математическим» факторам выбора проекции, и наоборот – для малых территорий и крупных масштабов более существенными становятся «географические» факторы.

Приведите примеры цилиндрических и конических изделий из древесины. Просмотр содержимого документа

Изготовление

конических

деталей

вручную

ТЕХНОЛОГИЧЕСКАЯ КАРТА - технологическая документация в виде карты, листка, содержащего описание процесса изготовления, операций обработки изделия, применяемого оборудования, инструментов .

Технологическая карта состоит из четырёх столбцов

Технологическая карта

№

п/п

Этапы обработки

Графическое изображение

Инструменты

Технология изготовления цилиндрических и конических деталей ручным инструментом

• Возможно, ваше проектное изделие будет иметь детали цилиндрической

и конической формы. Такие детали можно изготовить

с применением известных вам ручных инструментов

и приспособлений.

Изготовление

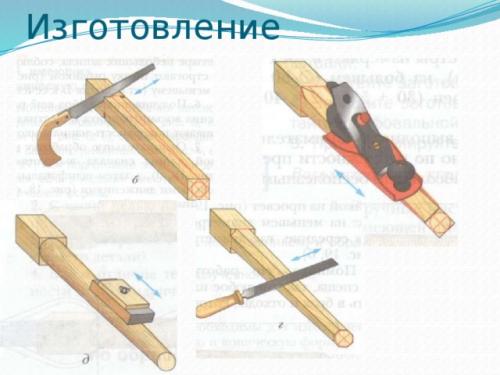
• Из обструганной заранее доски нужной толщины вырезают заготовку изделия.
• На т о р ц е заготовки на пересечении диагоналей определяют центр сечения и циркулем вычерчи- вают окружность

Заготовку строгают рубанком до разметочных линий (смотри рис. и получают восьмигранник.) (Можно строгать рёбра до получения шестнадцатигранника, чтобы ещё больше приблизитьформу ручки к цилиндрической форме).

Выполняют зачистку оставшихся рёбер рашпилем или напильником с грубой насечкой и окончательно обрабатывают ручку шлифовальной шкуркой . В процессе обработки и по окончании шлифовки следует измерить диаметр заготовки кронциркулем в нескольких точках по длине и в двух взаимно перпендикуляр ных сечениях. После измерения диаметра кронциркуль прикладывают к линейке и узнают замеренный размер.

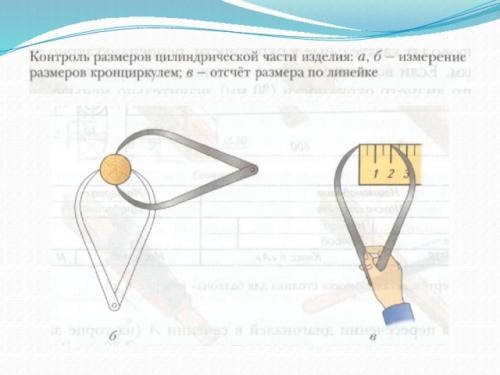
Коническая форма

• Детали небольшого диаметра можно изготовлять без предварительной разметки, но с соблюдением описанной выше технологии обработки. Рассмотрим технологию обработки заготовки в том случае, если необходимо получить из неё деталь, имеющую коническую форму.
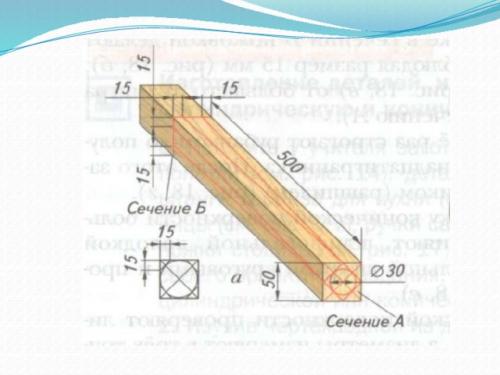
• На оструганном заранее бруске нужного размера размечают длину конической части.
• На пересечении диагоналей в сечении А (на торце заготовки) определяют центр и проводят окружность

• Затем проводят касательные к окружности, перпендикулярно диагоналям. Если восьмиуголь-ник в сечении не получается, из-за того, что диаметр окружности значительно меньше, чем размер сечения, то п р о с т о соединяют линиями середины сторон в сечении.
• Чтобы правильно выполнить разметку в сечении Б, на листе бумаги вычерчивают квадрат в масштабе 1 : 1 и вписывают в него окружность, после чего проводят касательные и получают восьмиугольник. Такой рисунок позволяет определить размеры восьмигранника. Эти размеры откладывают на заготовке в сечении Б и проводят продольные линии к сечению А.

Примеры цилиндрических деталей. Графическое изображение деталей цилиндрической формы

Изготавливаемые изделия, кроме прямоугольных деталей содержат и детали цилиндрической формы (ручки киянок, подсвечники и др.).

На токарном станке по дереву можно изготовить чаши, кубки, тарелки, солонки, ручки мебельные.

Они имеют цилиндрическую форму.

При выполнении чертежей простых деталей, имеющих цилиндрическую форму, можно ограничиться одним главным видом .

Знак диаметра и осевая линия на изображении свидетельствует о цилиндрической форме детали.

Другие виды показывают только в том случае, если на деталях есть элементы, форму которых трудно определить по одному виду.

Детали цилиндрической формы часто имеют такие конструктивные элементы, как фаски, галтели, пазы, буртики и др.

Размеры фаски на чертеже указывают записью типа 3х45°, где 3 – высота фаски (мм), 45° — угол , под которым она выполнена.

Чертеж изделия с конической поверхностью,
определение на чертеже уклона и конусности

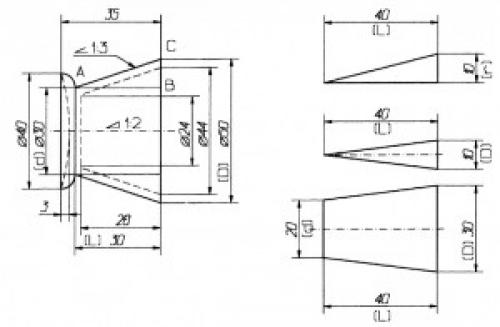
Изделия из древесины имеют наружную и внутреннюю коническую поверхность.

Для чертежей таких деталей обычно достаточно одного вида , на котором проставляют необходимые размеры и обозначения.

Они дают точное представление о форме и размерах детали.

На чертеже могут быть проставлены обозначения уклона и конусности .

Уклон (У) характеризует наклон образующей конуса к его оси.

Выражают величину уклона в виде простой дроби – отношения катетов треугольника, гипотенуза которого является образующей.

Например, чтобы понять, с каким уклоном находится линия АС по отношению к линии АВ, рассмотрим треугольник АВС.

Линия ВС в четыре раза короче линии АВ.

Следовательно, уклон прямой АС по отношению к прямой АВ составляет 1:4.

Для усечённого конуса уклон равен отношению разности радиусов оснований конуса к расстоянию между ними: У = (R-r)/L.

На чертеже изделия с конической поверхностью У = (25-15)/ 30 = 1:3.

Конусность К – это отношение диаметра основания конуса к его высоте: К=D/L.

Конусность детали в виде усечённого конуса определяют по формуле: К= (D-d)/L.

На чертеже конусность обозначается равнобедренным треугольником с вершиной, направленной в сторону вершины конуса.

Его проставляют над осевой линией конуса.