Применение теории графов к решению задач. Использование графов при решении задач
- Применение теории графов к решению задач. Использование графов при решении задач
- Связанные вопросы и ответы
- Задачи на графы с решением. Решение задач с помощью графа
- Логические задачи решаемые с помощью графов. Просмотр содержимого документа ««Применение графов к решению логических задач»»
- Использование графов при решении задач. Пояснительная записка
- Применение теории графов в экономике. ГРАФЫ И ОБЛАСТИ ИХ ПРИМЕНЕНИЯ
- Простые задачи на графы. Решение задач с помощью графов
Применение теории графов к решению задач. Использование графов при решении задач
В математике существует целый раздел — теория графов, который изучает графы, их свойства и применение. Матюша пока изучил основные понятия и некоторые способы решения задач с помощью графов. И с радостью делится с вами полученными знаниями. Видеосюжет построен следующим образом: теория, а затем практические задания. Для их выполнения ребятам необходимо взять листок бумаги, ручку или карандаш, а ещё может пригодиться линейка.
Граф — это множество точек, которые могут соединяться линиями.
Линии указывают на связь между двумя точками.
Точки называются вершинами графа.
А линии, которые связывают вершины, называются рёбрами графа.
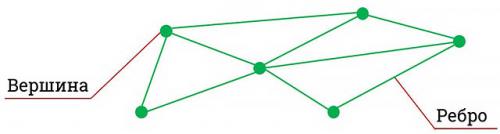
Знакомство с тремя видами графов будет происходить на примерах задач.
Неориентированный граф, в котором вершины соединены рёбрами без указания направлений.
Задача: между восемью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля — Юпитер; Земля — Меркурий; Меркурий — Марс; Марс — Венера; Уран — Сатурн; Юпитер — Нептун; Нептун — Марс.
Можно ли долететь на рейсовых ракетах с Земли до Урана?
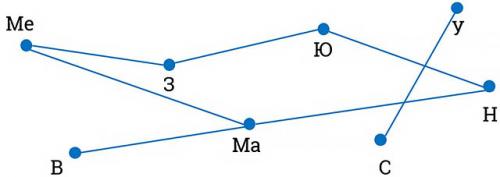
Ориентированный граф, в котором вершины соединены рёбрами с указанием направлений.
Задача: На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города, А в город Ж?
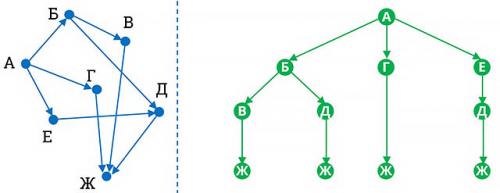
Взвешенный граф, в котором вершины соединены рёбрами, которые имеют вес.
Задача: между населёнными пунктами А, B, C, D, E построены дороги. Протяжённость дорог (в километрах) приведена в таблице.
Нужно определить длину кратчайшего пути между пунктами, А и D. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
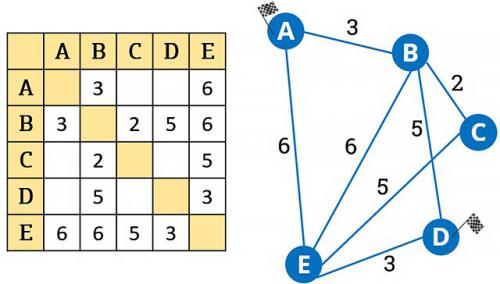
Рассмотренные теоретические знания и решённые задачи помогут ребятам справится с задачами, которые предложены для самостоятельного выполнения. Задачи будут даны на все виды графов, рассмотренные в первой части видеосюжета.

Матюша уверен, что ребята справятся с решением без проблем.
Связанные вопросы и ответы:
1. Что такое теория графов и как она применяется для решения задач
Теория графов - это раздел математики, изучающий свойства и взаимосвязи графовых структур, состоящих из вершин и ребер. Применение теории графов к решению задач заключается в моделировании реальных ситуаций с помощью графов и анализе их свойств для нахождения оптимальных решений. Например, задачи о маршрутах, сетевых связях, раскраске графов и многих других могут быть решены с помощью теории графов.
2. Как можно представить задачу на поиск кратчайшего пути с помощью теории графов
Задачу на поиск кратчайшего пути можно представить с помощью графа, где вершины представляют места, а ребра - дороги или пути между ними. Каждому ребру можно также присвоить вес, который может представлять расстояние, время или другую характеристику, которую требуется минимизировать. Затем применяются алгоритмы, такие как алгоритм Дейкстры или алгоритм A*, для поиска кратчайшего пути в графе.
3. Как теория графов применяется в задачах планирования
Теория графов может быть использована для моделирования процессов планирования, где вершины представляют задачи или события, а ребра - зависимости между ними. Например, в проектном менеджменте графы могут использоваться для построения сетевых диаграмм, где каждая вершина представляет активность, а ребра - связи между активностями. Алгоритмы теории графов могут быть применены для определения критического пути, распределения ресурсов и оптимизации времени выполнения задач.
4. Как теория графов помогает в задачах анализа сетей
Теория графов является ключевым инструментом для анализа сетей, таких как социальные сети, транспортные сети, сети связи и другие. Графы могут быть использованы для представления взаимосвязей между узлами в сети, а алгоритмы теории графов позволяют анализировать такие свойства сетей, как степень связности, центральность узлов, поиск сообществ и транзитивность.
5. Как теория графов применяется в задачах оптимального покрытия
В задачах оптимального покрытия, таких как задача о покрытии множества, теория графов может быть использована для представления элементов и их взаимосвязей с помощью графа. Затем применяются алгоритмы для нахождения минимального покрытия графа. Такие решения могут быть применены, например, для оптимизации использования ресурсов или распределения задач между исполнителями.
6. Как теория графов применяется в задачах раскраски графов
В задачах раскраски графов, теория графов используется для определения минимального количества цветов, необходимых для окраски вершин графа таким образом, чтобы соседние вершины имели разные цвета. Раскраска графов может быть применена, например, для планирования расписания или связана с проблемами графовой теории, такими как теорема о четырех красках.
7. Как теория графов применяется в задачах маршрутизации и сетевого планирования
Теория графов является основой для задач маршрутизации и сетевого планирования. Графы могут быть использованы для представления сетевых структур, таких как дорожные сети или сети связи, а алгоритмы теории графов могут быть применены для нахождения оптимальных маршрутов, планирования передачи данных или оптимизации расходов ресурсов. Такие решения на основе теории графов способствуют более эффективной и надежной работе сетевых систем.
Задачи на графы с решением. Решение задач с помощью графа
Теория графов применяется при решении задач из многих предметных областей: математика, биология, информатика
Мне нравится Проект нравится 23 участникам
1736 год, г.Кёнигсберг. Через город протекает река Прегеля. В городе - семь мостов, расположенных так, как показано на рисунке выше. С давних времен жители Кенигсберга бились над загадкой: можно ли пройти по всем мостам, пройдя по каждому только один раз? Эту задачу решали и теоретически, на бумаге, и на практике, на прогулках - проходя по этим самым мостам. Никому не удавалось доказать, что это неосуществимо, но и совершить такую «загадочную» прогулку по мостам никто не мог.
Разрешить проблему удалось знаменитому математику Леонарду Эйлеру. Причем, он решил не только эту конкретную задачу, но придумал общий метод решения подобных задач. При решении задачи о Кенигсбергских мостах Эйлер поступил следующим образом: он "сжал" сушу в точки, а мосты "вытянул" в линии. Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют ГРАФОМ .
Граф – это совокупность непустого множества вершин и связей между вершинами. Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами.
Виды графов:
1. Ориентированный граф (кратко орграф ) — рёбрам которого присвоено направление.
2. Неориентированный граф - это граф , в котором нет направления линий.
3. Взвешенный граф – дуги или ребра имеют вес (дополнительная информация).
Решение задач с помощью графов:
Задача 1.
Решение: Обозначим ученых вершинами графа и проведем от каждой вершины линии к четырем другим вершинам. Получаем 10 линий, которые и будут считаться рукопожатиями.
Задача 2.
На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.
Решение:
Вершины графа - это деревья, обозначенный первой буквой названия дерева. В данной задача два отношения: “быть ниже” и “быть выше”. Рассмотрим отношение “быть ниже” и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.
Задача 3.
У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо?
Решение:
Ниже представлен разбор задач.
Логические задачи решаемые с помощью графов. Просмотр содержимого документа ««Применение графов к решению логических задач»»
Краткое изложение факультативного занятия на тему: «Применение графов к решению логических задач»
Цель: разобрать закономерности решения логических задач с помощью графов.
Ход занятия:
Объяснение учителем.
Решение логических задач с помощью графов.
Подведение итогов.
Домашнее задание.
Основой применения графов для решения логических задач служит выявление и последовательное исключение логических возможностей, задаваемых условиями задач. Это выявление и исключение логических возможностей часто может быть истолковано с помощью построения и рассмотрения соответствующих графов.
Задача 1.
Из трех человек, стоящих рядом, один всегда говорит правду (правдивый), другой всегда лжет (лжец), а третий, смотря по обстоятельствам, говорит правду или ложь («дипломат»). У стоящего слева спросили: «Кто стоит рядом с тобой?» Он ответил: «Правдолюб». Стоящему в центре, задали вопрос: «Кто ты?», и он ответил: «Я дипломат». Когда у стоящего справа спросили: «Кто стоит рядом с тобой?», он ответил: «Лжец». Кто где стоял?
Если в данной задаче ребро графа будет соответствовать месту, занимаемому тем или иным человеком, то нам могут представиться следующие возможности.
Рассмотрим первую возможность. Если «правдолюб» стоит слева, то рядом с ним, судя по его ответу, находится «правдолюб». У нас же стоит лжец. Рассмотрев таким образом все остальные возможности, мы придем к выводу, что расстановка «дипломат», «лжец», «правдолюб» удовлетворяет задаче. Действительно, если «правдолюб» стоит справа, то, по его ответу, рядом с ним «лжец», что выполняется. Стоящий в центре заявляет, что он «дипломат», и следовательно, лжет, а стоящий справа также лжет. Таким образом все условия задачи выполнены. В качестве задачи второго типа можно предложить следующую.
Задача 2.
В пяти корзинах лежали яблоки пяти разных сортов. Яблоки первого сорта лежат в корзинах Г и Д; яблоки второго сорта - в корзинах А. Б, Г; в корзинах А, Б, В имеются яблоки пятого сорта, в корзине В имеются к тому же яблоки четвертого сорта, а в корзине Д-третьего. Пронумеруйте каждую корзину так, чтобы в корзине №1 были яблоки первого сорта (хотя бы одно); в корзине № 2-второго и т.д.
Решение: Составим граф:
Ответ: №1-Г; №2-А или №2-Б; №3-Д; №4-В; №5-Б или №5-А
Возникает вопрос: так ли уж нужны были графы в этой задаче? Разве нельзя прийти к решению логическим путем? Можно, но графы придали условия наглядность, упростили решение.
Задача 3.
В обеденный перерыв предприниматели разговорились, кто сколько газет читает. Выяснилось, что каждый выписывает и читает две и только две газеты, каждую газету читают пять человек, и любая комбинация читается одним человеком. Сколько названий газет выписывают предприниматели? Сколько всего было человек?
Решение этой задачи достигается построением следующего графа, где каждая вершина обозначает соответствующую газету и соответственно 5 подписчиков, а каждое ребро будет соответствовать одному подписчику.
Суть метода решения этой и подобных ей задач состоит в установлении связей между множеством вершин и множеством ребер графа.
Следовательно, в данной задаче предприниматели выписывают шесть наименований газет. Всего предпринимателей:
6*(6-1)/2=15 чел.
Полезно решать логические задачи разными методами. Например, следующую задачу можно решить способом логических квадратов и с помощью графов.
Задача 3.
Три ученицы - Аня, Валя. Катя - участвовали в новогоднем бале - маскараде. Одна из них была в красном костюме, другая - в белом, третья - в синем. Если сказать, что Аня была в красном, Валя – не в красном, и Катя –не в синем, то одно из этих утверждений будет верным, а два других –неверными. В каком костюме была каждая из учениц?
Логический квадрат для этого случая имеет вид:
Графы для этой задачи имеют вид.
Использование графов при решении задач. Пояснительная записка
Актуальность. Основной задачей школы является не подача детям большого объёма знаний, а обучение учащихся самим добывать знания, умению перерабатывать эти знания и применять их в каждодневной жизни. Поставленные задачи может решить ученик, обладающий не только умением хорошо и много работать, но и ученик с развитым логическим мышлением. В связи с этим во многие школьные предметы вложены различного типа задачи, которые и развивают у детей логическое мышление. Решая эти задачи, мы применяем различные приёмы решения. Одни из приёмов решения – это граф.
« Графы » имеют корень греческого слова « графо », что значит « пишу ». Тот же корень в словах « график », « биография », « голография ».
Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов. Толчок к развитию теория графов получила на рубеже XIX и XX столетий, когда резко возросло число работ в области топологии и комбинаторики, с которыми её связывают самые тесные узы родства. В последнее время графы и связанные с ними методы исследований пронизывают на разных уровнях едва ли не всю современную математику. Графы используются в теории планирования и управления, теории расписаний, социологии, математической лингвистике, экономике, биологии, медицине. Как более жизненный пример можно взять использование графов в геоинформационных системах. Существующие или вновь проектируемые дома, сооружения, кварталы и т.п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т.п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут. Теория графов быстро развивается, находит всё новые приложения и ждёт молодых исследователей.
Применение теории графов в экономике. ГРАФЫ И ОБЛАСТИ ИХ ПРИМЕНЕНИЯ
Хиневич Е.С. 1
1 МБОУДО «ДДТ «Дриада» г.Снежногорска Мурманской области
Текст работы размещён без изображений и формул.Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
ВВЕДЕНИЕ«В математике следует помнить не формулы, а процесс мышления…»
Е. И. Игнатьев
Теория графов в настоящее время является интенсивно развивающимся разделом математики. Это объясняется тем, что в виде графовых моделей описываются многие объекты и ситуации, что очень важно для нормального функционирования общественной жизни. Именно этот фактор определяет актуальность их более подробного изучения. Поэтому тематика данной работы достаточно актуальна.
Цель исследовательской работы: выяснить особенности применения теории графов в различных областях знаний и при решении логических задач.
Цель определила следующие задачи:
познакомиться с историей теории графов;
изучить основные понятия теории графов и основные характеристики графов;
показать практическое применение теории графов в различных областях знаний;
рассмотреть способы решения задач с помощью графов и составить собственные задачи.
Объект исследования: сфера деятельности человека на предмет применения метода графов.
Предмет исследования: раздел математики «Теория графов».
Гипотеза. Мы предполагаем, что изучение теории графов может помочь учащимся решать логические задачи по математике, что определит их дальнейшие интересы.
Методы исследовательской работы:
В ходе нашего исследования были использованы такие методы, как:
1) Работа с различными источниками информации.
2) Описание, сбор, систематизация материала.
3) Наблюдение, анализ и сравнение.
4) Составление задач.
Новизна работы заключается в авторском составлении задач по теме исследования и нахождении практического использования теории графов в современном мире.
Теоретическая и практическая значимость данной работы определяется тем, что результаты могут быть использованы на информатике, математике, геометрии, черчении и классных часах, а также для широкого круга читателей, заинтересованных данной темой. Исследовательская работа имеет выраженную практическую направленность, так как в работе автором представлены многочисленные примеры применения графов во многих областях знаний, составлены свои задачи. Данный материал можно использовать на факультативных занятиях по математике.
ГЛАВА I. ТЕОРЕТИЧЕСКИЙ ОБЗОР МАТЕРИАЛА ПО ТЕМЕ ИССЛЕДОВАНИЯ
В математике «граф» можно изобразить в виде картинки, которая представляет собой некоторое количество точек, соединенных линиями. «Граф» происходит от латинского слова «графио» – пишу, как и известный дворянский титул.
В математике определение графа дается так:
Термин «граф» в математике определяется следующим образом:
В качестве примеров графов могут выступать чертежи многоугольников, электросхемы, схематичное изображение авиалиний, метро, дорог и т.п. Генеалогическое дерево также является графом, где вершинами служат члены рода, а родственные связи выступают в качестве ребер графа.
Примеры графов
Число ребер, которое принадлежит одной вершине, называется . Если степень вершины нечетное число, вершина называется – нечетной . Если степень вершины число четное, то и вершина называется четной
Вершина графа
– это граф, состоящий только из изолированных вершин, не соединенных ребрами.
– это граф, каждая пара вершин которого соединена ребром. N-угольник, в котором проведены все диагонали, может служить примеров полного графа.
Если в графе выбрать такой путь, когда начальная и конечная точка совпадают, то такой путь называется Если прохождение через каждую вершину графа происходит не более одного раза, тоназывается .
Если в графе каждые две вершины связаны ребром, то это граф. Граф называется , если в нем есть хотя бы одна пара несвязанных вершин.
Если граф связанный, но не содержит циклов, то такой граф называется .
– это такая последовательность, в которой каждые два соседних ребра, имеющих одну общую вершину, встречаются только один раз.
Вершина называется графа, если расстояние между вершиной и любой другой вершиной является наименьшим и из возможных. Такое расстояние есть графа.
Максимально возможное расстояние между двумя любыми вершинами графа называется графа.
Если внимательно посмотреть на географическую карту, то можно увидеть железные или шоссейные дороги, которые являются графами. Кроме этого на катре есть граф, который состоит из границ между странами (районами, областями).
Простые задачи на графы. Решение задач с помощью графов
Урок 6. Математика и игры 3–4 классы
В данном
Получите невероятные возможности
Прежде чем приступить к решению задач, стоит сказать, что графы, о которых пойдёт речь, к аристократам былых времён никакого отношения не имеют. У наших графов в корне есть греческое слово «графо», что значит «пишу». Этот же корень («граф») встречается, например, в словах «график, «биография», «орфография» и некоторых других.
Давайте выясним понятие графа на примере решениязадачи.
В первенстве класса по настольному теннису шесть участников: Андрей, Саша, Вова, Оля, Дима и Лена. Каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Сашей, Олей и Леной; Саша, как уже говорилось, с Андреем и ещё с Олей; Вова – с Олей, Димой и Леной. Сколько игр уже проведено и сколько ещё осталось?
Итак, изобразим данные этой задачи в виде схемы. Участников первенства обозначим точками, расположив их по окружности: Андрей – А, Саша – ЭС, Вова – ВЭ, Оля – О, Дима – ДЭ, Лена – ЭЛЬ.
Если двое участников уже сыграли между собой, то будем соединять, обозначающие их точки отрезками. В условии задачи сказано, что Андрей сыграл с Сашей, Олей и Леной.
Мы уже видим, что Саша сыграл с Андреем, а ещё он сыграл с Олей.
Вова сыграл с Олей, Димой и Леной.
Получившаяся схема называется графом . Точки А, С, В, О, ДЭ, Л называются вершинами графа . Отрезки, которые соединяют вершины графа, называются рёбрами графа . Каждое ребро соединяет две вершины графа.
При этом обратите внимание, что точки, в которых пересекаются рёбра графа, не являются его вершинами.
У графа 7 рёбер. Это означает, что к настоящему моменту было проведено 7 игр.
Чтобы найти количество игр, которые осталось провести, продолжим построение этого графа так, чтобы из каждой точки были проведены рёбра ко всем остальным точкам. Но для того, чтобы потом легче было подсчитать количество добавленных рёбер, рисовать их будем другим цветом.
Итак, известно, что Андрей сыграл с Сашей, Олей и Леной. А значит, он не играл с Вовой и Димой.
Также известно, что Саша сыграл с Андреем и с Олей, а значит, он не сыграл с Вовой, Димой и Леной.
Вова сыграл с Олей, Димой и Леной. Получается, что он не сыграл с Андреем и Сашей. Но соответствующие отрезки уже проведены.
Оля сыграла с Андреем и Сашей, а также с Вовой. Это значит, что она ещё не сыграла с Димой и Леной.
Дима сыграл только с Вовой. Ему предстоит сыграть с Олей, Сашей и Андреем, но эти отрезки мы уже провели. Осталось провести отрезок от Димы к Лене.
Лена сыграла с Андреем и Вовой. Ей предстоит сыграть с Димой, Олей и Сашей, но эти отрезки мы уже провели. Больше ничего добавлять не надо.
Мы добавили 8 рёбер. Это значит, что осталось провести ещё 8 игр. Получается, что ответ на вопрос задачи будет таким: проведено 7 игр, осталось провести 8 игр.
Отметим, что граф для одной и той же задачи можно нарисовать разными способами. И наоборот, для разных задач можно нарисовать одинаковые по виду графы.
Также отметим, что иногда рёбра удобнее изображать не отрезками, а «дугами».
Граф можно представить как набор пуговиц, некоторые из которых соединены нитями. Пуговицы – это вершины графа, нити – его рёбра.
При этом, где именно расположены пуговицы, и как проходят нити не важно, ведь граф от этого не меняется. Важно то, какие пары пуговиц (то есть вершин графа) соединены нитями.
Но при решении задач, подобных приведённой, удобнее всё-таки располагать вершины по окружности. Тогда при проведении рёбер рисунок получается не таким запутанным.
Если из вершины графа выходит чётное количество рёбер, то её называют чётной . А если из вершины графа выходит нечётное количество рёбер, то её называют нечётной .
Посмотрите на такой граф.
У него вершины 1 и 4 являются нечётными , так как из них выходят по 3 ребра.